Malaria and Simulations for Health Policy

Human Travel Patterns and Imported Malaria Cases

In collaboration with the Bioko Island Malaria Elimination Program, we have quantified the influence of human travel on malaria transmission patterns on Bioko Island in Equatorial Guinea. Click here to read more about the project, in which we used a combination of mapping and modeling techniques to argue that there is strong evidence of elevated malaria risk among people who travel from Bioko Island to mainland Equatorial Guinea.

Here is a poster on building and utilizing simulation models of malaria transmission to quantify the influence of human travel on malaria transmission patterns on Bioko Island, presented in 2019 at the American Society for Tropical Medicine and Hygiene conference. An earlier version of this analysis, first completed in 2018, I presented at the 2019 Institute for Disease Modeling Consortium (slides here).

Modeling with Human Travel Data

Through my work on travel and importations in collaboration with the Bioko Island Malaria Elimination Program, I have investigated how one can use various mechanistic models to represent human population movement patterns and have come to realize that one must be very mindful of how one incorporates human movement into mechanistic models of infectious disease. Specifically, infectious disease models may have outcomes that are sensitive to how the modeler chooses to represent movement within the model independent of infection model choice or data used for parameterizing the model.

I presented preliminary work on this model sensitivity at the Netsci 2019 conference (poster here), and gave a talk at the 2019 epidemics conference (slides here).

Structural Analysis of Networks

Network Assembly of Scientific Collaborations

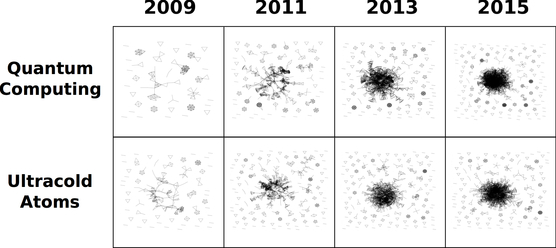
How do scientific fields develop? How does the underlying social structure of scientific research change as a little-known idea or discovery grows into a well-established new field?

The work of David Kaiser and Luis Bettencourt has shown that over time, as more researchers enter a new field and work with others, enough collaborative ties form such that the initial cohort of disjointed research groups joins together to form a giant, densely connected component. (One can see two examples of this process in the co-authorship networks of quantum computing and ultracold atoms, shown above.) The densely connected component formation represents social restructuring on a global scale, as scientists establish new research groups; new collaborations develop; and the community agrees upon a set of shared tools, techniques, and terminology for communicating ideas.

How robust is this pattern? To answer this question, I have used standard topic modeling software (Mallet) to sort the articles available on the arXiv according to scientific subtopics. I find that the majority of topics detected with Mallet reflect real, established scientific fields, and that for many of these topics we do find the emergence of a densely connected giant component in the corresponding co-authorship network. These results are quantitative evidence of the social restructuring that occurs as scientific fields develop.

This project began in collaboration with others as part of the 2015 Complex Systems Summer School at the Santa Fe Institute. I presented a poster on the subject at the 2015 International Conference on Computational Social Science. (Manuscript currently in preparation.)

Forthcoming article is currently under review

Measuring Text Reuse Patterns in Articles on arXiv.org

The arXiv is an online repository of scientific articles available publicly at arxiv.org. At the time when this project began (Summer 2012), administrators of the arXiv had become increasingly aware of instances of authors repeatedly copying text from previously published material. This included cases of plagiarism as well as less egregious but still problematic cases of authors repeatedly submitting the same material with minor superficial changes. Needless to say, arXiv administrators were concerned about this reported behavior, and wanted to know more about the problem. How frequently did authors use copied material? Was copying behavior restricted to a particular subset of authors, or did everybody reuse text sometimes? Did articles featuring copied material garner much attention in terms of citations?

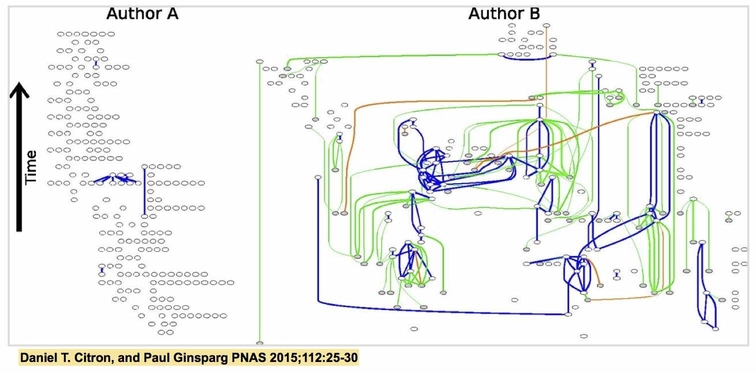
My role in the project was to compile the data into a format where it could be analyzed in a meaningful way. I created a "text overlap network," in which nodes represented articles and edges represented pairwise text overlap between the two articles. In this new format the data could be easily visualized and explored using standard network analysis tools. This enabled us to answer a lot of questions regarding the behavior of the community of scientists submitting to arXiv. For example, we found that the vast majority of authors did not reuse text from others' articles, that instead only a few authors habitually reused text. We also discovered that articles containing a large amount of copied material tended to earn fewer citations, suggesting that these articles were produced on the fringes of the scientific community.

You can find an arXiv preprint of our paper here and the online version published in PNAS here. This work was mentioned in a Science news article as well as in The Atlantic. In 2013, I presented on this topic as part of the STEM Graduate Student Summer Colloquium at Cornell University (slides here).

Dynamical Processes on Networks

Network Heterogeneity and Spontaneous Extinction of Endemic Disease

Numerous studies have suggested that the structure of the contact network in a susceptible population is crucial for understanding the progression of an outbreak of disease, as well as suggesting strategies for combating epidemics. In the context of recurrent or endemic disease, the notion of "critical community size" was introduced to explain why larger populations tend to sustain outbreaks for longer periods of time than smaller populations. The random events that make up an epidemic- infection, recovery, migration- lead to stochastic fluctuations. Smaller populations have larger fluctuations, making it more likely for a fluctuation to spontaneously send the number of infected individuals to zero.

The role of fluctuations and their relationship to spontaneous extinction is not yet understood in the context of contact networks: the contact networks underlying the interactions between different members of a population may vary dramatically between different types of populations. How does a network's structure affect its potential for sustaining endemic diseases? I have used simulations in conjunction with analytical moment closure techniques to explore this question, and have found that a graph's structural heterogeneity can have significant effects on the size of fluctuations and the rate of extinction.

My poster on this topic titled "Accounting for Fluctuations in Stochastic SIRS Model on Networks" from the Advances in Discrete Networks workshop I attended at the University of Pittsburgh in December 2014 can be found here

Simulating Disease Dynamics on Networks

I have developed a number of Python scripts for simulating stochastic models of disease dynamics in fully mixed populations and on networks. I have used these simulations extensively for exploring the stochastic SIRS model described above.

Side Projects

A few other projects, analyzing and visualizing data.